Supplemetnal information to provide detailed information on the minimal tiling path algorithm.
Supplemental Table IV.
Adjustable parameters of the PickMTP algorithm:
Constraint
Description
Default value
E-value (BLAST)
BLAST expectation value.
1e-100
minId
Minimum BLAST % identity of a hit.
97%
minScore
Minimum BLAST bit score of a hit.
400
limitBESHits
If true, discard all hits where more than one seqCtg hits a BES
True
Orientation of hits
Discards all pairs where both hits have the same orientation.
--
olapFudge
Amount of difference allowed between estimated FPC overlap
and the overlap based on the BES hits to the seqCtg
20,480 bases
seqCtgDist
Maximum distance between BES hits along the seqCtg.
50,000 bases
maxSpan
Maximum distance between extremities (CB units) for a
set of clone pairs from one seqCtg.
450kb
onlyPosOlap
Only consider pairs with positive overlap.
False
anchorOnly
Only consider anchored contigs.
False
The following describes the 5 steps used by PickMTP for selecting an MTP:
1. BLAST the draft sequence against the BES library: BLAST searches are performed using the previously described BSS feature found in FPC V5 and higher. The draft sequence contigs are BLASTed against the BES library of clones in FPC. The summary report that is generated associates BES hits with their clone and FPC contig number. After the report is filtered for hits of low confidence, it becomes the input for the next step.
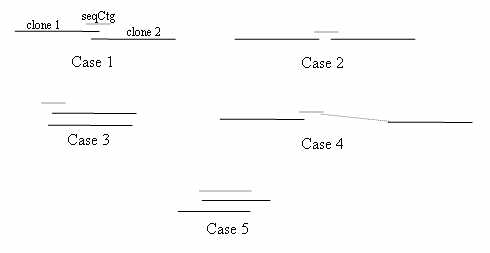
2. Compile a list of overlapping clone pairs: Any pair of BESs from different clones hitting a common sequence contig is a potential MTP pair. Most false positive pairs can be removed by examining the FPC map; if a pair contains clones from two different contigs, they are immediately rejected. (NB A pair of clones that are at the ends of two different contigs can be used to identify contigs to merge, a procedure not covered in this paper). The remaining pairs fit one of the five cases depicted below.

If a sequence contig hits the BES of two clones close to one another in the map, either the
clones overlap (case 1) or are bridged clones, where the definition of bridged clones
is that they do not overlap but are bridged by a sequence contig that can be used to fill
the gap (case 2). If there is sufficient coverage by BES and draft sequence, it may not be
necessary to use bridging clones, in which case such pairs may be rejected. The overlaps
depicted in cases 3-5 are rejected, as follows:
Case 3 occurs when two left ends or two right ends of the clones hit the sequence contig,
and the sequence contig does not span the clones; hence, the clones overlap by an unacceptable
amount. To eliminate this case, we consider the orientation of the hits with respect to the
sequence contig (see Figure 6 in accompanying paper). The true orientation of the clone in
relation to the chromosome is not known, therefore, the true left and right end are not known.
However, the BES is always read and written starting from the end of a clone and progressing
towards the middle, and the orientation of the BES pair is known with respect to the sequence
contig. Therefore, a case 1 or case 2 hit requires that the BES of one clone be reverse
complemented to match the sequence contig, while the BES of the other clone may not be.
BLAST tells us whether the BES has been reverse complemented by labeling the hits
as "Plus/Plus" (no reverse complement) or "Plus/Minus" (reverse complement), and this
is also shown in the BSS output in the "RC" column. A pair is rejected if it has
two "Plus/Plus" or two "Plus/Minus" hits, as such an instance indicates a case 3 pair.
Case 4 occurs when a sequence contig hits two clones that may be in the same contig, but
the sequence contig contains a repetitive sequence and hits multiple times in a contig.
To eliminate resulting bad pairs, the sequence contig-BES overlap and FPC clone overlap
are compared. The sequence contig-BES overlap is the distance between the locations of
the two BESs on the sequence contig. The FPC clone overlap is based on the overlap of the
clones in FPC, which is measured in terms of CB (consensus band) units; one CB is approximately
one band. By using the conversion of 1 CB unit = 4096 bases, we can predict the approximate
clone overlap. However, since 4096 is an approximation of the band size and the overlap in CB
units is approximate (Soderlund et al. 2000), the FPC overlap in bases is a very rough approximation,
though it still can be used to disqualify obvious discrepancies. The parameter that limits how much
the sequence contig-BES and FPC clone overlaps vary is called the overlap fudge factor. In a related
scenario, a sequence contig producing pairs in multiple contigs, or in different regions of a single
contig, raises ambiguity over which pairs are correct. Hence, all pairs for a given sequence contig
must occur in only one contig, and the pairs must be located in the same region of the contig;
otherwise, the sequence contig is rejected. Finally, the draft query sequence is generally expected
to contain only unique sequence contigs, so no two sequence contigs should hit the same BES. Such
an occurrence indicates false positive hits, and all such hits should be discarded.
Case 5 occurs when the draft sequence contains very long sequence contigs, such that a pair may
overlap more than suitable for a minimal tiling path. All pairs are rejected that have an overlap
of more than seqCtgDist bases (note, in the shortest paths algorithm described below, large overlaps
are avoided when possible).
The rules are applied in the order given in Table 1. The pairs passing all tests are candidate
MTP pairs and are written to a file that is the input for a C program used to pick expressways
based on the clone pairs.
3. Identify all possible expressways: The "single source shortest paths problem" is defined as
follows: given a directed graph G = (V, E) in which each edge has a positive weight and one
vertex is specified as the source, determine the cost of the shortest path from the source
vertex to every other vertex in V, where the length of a path is the sum of the weights on the
edges of the path (Aho et al. 1983). The algorithm is used to compute all possible expressways
for each contig. There are four steps to building the expressways: (i) construct a set of
disconnected DAGs (Directed Acyclic Graphs), (ii) find the set S of source vertices and the
set T of target vertices for each subgraph, (iii) run the shortest paths algorithm on each
source si in S, and (iv) save each shortest path Pij from a source si to a target tj as an
expressway.
The set of DAGs are constructed as follows: every clone that is in a candidate MTP pair is
a vertex in V, and there exists an edge in E between each candidate MTP pair. The edge is
directed from the left to the right clone, as defined by the FPC map. The edge weight is
determined by the absolute difference between the positions of the BESs on the sequence contig,
and the weight for bridging clones is multiplied by a factor of 10 in order to make selecting
overlapping clones take precedence over bridging clones. Below is shown how graphs are constructed
from the pair information. Note that this step creates many subgraphs, as will be explained in
step 4.
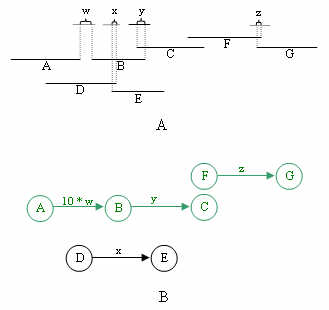
Once the graphs are constructed, all vertices with no incoming edges are marked as source vertices. From each source si, the vertex representing a clone furthest to the right of the contig, and reachable from si, is marked as the target. The shortest paths algorithm is run on each subgraph for all S source vertices. Every shortest path Pij from source si to target tj is saved as an expressway.
4. Greedily pick the set of expressways that span each contig: Once all possible expressways have been identified for each contig, a subset is picked to cover that contig. Optimally, there will be one expressway spanning the entire contig. Unfortunately, this is usually not the case, as gaps in the draft sequence, poor quality BESs, missing BESs, incorrectly discarded pairs, and sparse clone coverage can all contribute to non-contiguous expressways through contigs. With a 20X map coverage and 150kb clones, the BESs will be distributed at an average distance of 3750 (150,000/(20 * 2)) bases. With an average BES length of 650, we are left with average spaces between BESs of 3100 bases. Consequently, it is very possible for a reasonably sized sequence contig to hit zero or one BES, thus producing no pairs for that region. Also, an identified pair p may occur in the middle of a clone that is part of a pair assigned to an expressway, yet pair p starts a new expressway, since no sequence evidence exists to link the two pairs. The clones within an expressway have minimal overlap, so the primary objective is to pick long expressways to span the contig. A secondary objective is to reduce the number of junctions and gaps, as junctions will have larger overlaps and need to be inspected manually, and gaps require that clones be picked manually to cover the gap. A simple way to meet both objectives is to pick expressways to cover a contig based on their length. In this greedy approach, the longest expressway is picked to cover the contig between the left and right endpoints of the expressway. Subsequent expressways will be picked in the order of their length to further cover the contig, given that at least 80% of their span is not yet covered by any previously included expressways. Therefore, it is guaranteed that the longest expressways will be given precedence and gaps are reduced by also including shorter expressways and permitting some overlap between expressways. It should be noted that this method does not guarantee optimal results. However, its simplicity and good results make it a worthwhile choice.
5. Remove excess clones: By allowing expressways to overlap, we occasionally run into the situation where a pair of expressways overlaps by more than one clone. In such a case, the expressway overlap can be reduced, but still kept above a minimum 5 CB units, by removing one or more clones from the end of either the left or right expressway.
Aho, A, Hopcroft, J., and Ullman, J. 1983. Data Structures and Algorithms, pp. 203-208. Addison-Wesley, Reading, Massachusetts.
Soderlund, C., Humphrey, S., Dunhum, A., and French, L. 2000. Contigs built with fingerprints, markers and FPC V4.7. Genome Research 10:1772-1787.